CINÉTICA E MODELAGEM MATEMÁTICA DA SECAGEM DA PASTA DE BETERRABA

Capítulo de livro publicado no livro do VIII ENAG E CITAG. Para acessa-lo  clique aqui.

DOI: https://doi.org/10.53934/9786585062046-55

Este trabalho foi escrito por:

Francisca Jilkelly Costa Ferreira; Ingrid Raissa Pascoal Anacleto  ; Elisabete Piancó de Sousa *; Dyego da Costa Santos ; Raimunda Valdenice da Silva Freitas ; Gustavo Santos de Lima ; Luciene Xavier de Mesquita Carvalho  

*Autor correspondente: Elisabete Piancó de Sousa – Email: [email protected]

Resumo: Com o aumento de produção da beterraba (beta vulgaris), faz-se necessário o uso de alternativas viáveis para a sua conservação e, nesse contexto a secagem convectiva se torna uma forma simples e de baixo custo, sendo utilizadas em diversas frutas e hortaliças. Com isso, objetivou-se realizar a cinética e modelagem matemática da pasta de beterraba em diferentes temperaturas de secagem (60, 70 e 80 ºC), com espessura de 0,5 cm e com velocidade do ar de 1,0 m/s. Foram realizadas pesagens periódicas até massa constante e, posteriormente, os dados obtidos a partir da secagem foram ajustados aos diferentes modelos matemáticos tradicionalmente utilizados na secagem de produtos apículas, no qual observou-se que o modelo Page foi considerado como o modelo que melhor se ajustou aos dados experimentais na predição das curvas de secagem da pasta de beterraba, pois apresentou o melhor ajuste aos dados experimentais.  Os coeficientes de determinação (R²) que mais se aproximaram de 0,99 e os baixos valores de X² e de DQM são indicativos de alta qualidade de ajuste. Portanto, representação do processo de secagem é fundamental, pois as informações resultantes são de grande valia para o desenvolvimento de equipamentos e previsão de tempos de secagem de frutas e hortaliças.

Palavras–chave: Beta vulgaris; difusão efetiva; secagem convectiva

Abstract: With the increase in beet (beta vulgaris) production, it is necessary to use viable alternatives for its conservation and, in this context, convective drying becomes a simple and low-cost way, being used in various fruits and vegetables. Thus, the objective was to perform the kinetics and mathematical modeling of the beet paste at different drying temperatures (60, 70 and 80 ºC), with a thickness of 0.5 cm and an air velocity of 1.0 m/s. Periodic weighings were carried out until constant mass and, later, the data obtained from the drying were adjusted to the different mathematical models traditionally used in the drying of bee products, in which it was observed that the Page model was considered as the model that best fitted. to the experimental data in the prediction of the drying curves of the beet paste, as it presented the best fit to the experimental data. The coefficients of determination (R²) that were closest to 0.99 and the low values ​​of X2 and DQM are indicative of a high quality of fit. Therefore, representation of the drying process is essential, as the resulting information is of great value for the development of equipment and prediction of drying times for fruits and vegetables.

Keywords: Beta vulgaris; effective diffusion; convective drying

INTRODUÇÃO

 A beterraba (Beta vulgaris) é um tubérculo nutritivo que é caracterizada pela sua cor roxa avermelhada e a sua doçura proeminente. É uma raiz de uma espécie de planta herbácea e é encontrada em países de clima temperado. No Brasil sua produção está localizada principalmente no sudeste (42%) e sul (35%). A sua coloração se deve a presença de um pigmento natural chamado betalaínas, que além de melhorar a aparência do vegetal ainda contribui para a saúde de quem o consome, possuindo ainda minerais, vitaminas, além de ter boas fontes de fibras dietéticas (1). 

De acordo Oliveira et al.(2) uma alternativa para aumentar a estabilidade de hortaliças é por meio da secagem, pois ocorre a remoção significativa do teor de água por meio da dessecação, na qual reduz os riscos de contaminação, deterioração e reações enzimáticas. Um método viável para indústria de alimentos e obtenção de produtos secos é a secagem artificial por convecção, sendo um método que requer um baixo custo e de fácil acesso. O processo de secagem é muito importante na tecnologia que proporciona a produção de alimentos de alta qualidade, permitindo a preservação de propriedades químicas e físicas, reduzindo o teor de água para níveis seguros para armazenamento, para que o produto possa ser utilizado em períodos em que a hortaliça e/ou fruto não é produzido (3).

Um fator importante da secagem é a cinética de secagem. O comportamento da cinética de secagem de produtos agrícolas pode ser representada por meio dos modelos matemáticos, como foi reportado por Resende et al.(4). Esses modelos podem ser teóricos, que considera apenas a resistência interna, a transferência de calor e a água entre o produto e o ar quente e os modelos semi teóricos, e os empíricos, que consideram somente a resistência interna, a temperatura e a umidade relativa do ar de secagem (5).

A cinética fornece informações sobre o comportamento da transferência de calor e massa entre o produto e o agente de secagem, normalmente o ar, e pode ser descrita por modelos matemáticos. A utilização desses modelos para representar o processo de secagem é fundamental, pois as informações resultantes são de grande valia para o desenvolvimento de equipamentos e previsão de tempos de secagem (6). Para Santos et al. (1) que estudaram a secagem convectiva do quiabo em fatias, nas temperaturas de 50, 60, 70 e 80 °C; os modelos matemáticos ajustados aos dados experimentais e aplicados foram os seguintes: Aproximação da difusão, Henderson & Pabis, Logarítmico, Midilli, Newton, Page e Thompson, os autores identificaram que dentre os modelos matemáticos utilizados, o modelo de Midilli apresentou os melhores parâmetros de ajustes aos dados experimentais. Pereira et al. (7) realizaram a secagem da polpa de tucumã na espessura de 4 mm e nas temperaturas de 30, 40, 50 e 60 °C, onde  desenvolveu-se ajustes de diferentes modelos matemáticos aos dados experimentais, portanto os modelos matemáticos de Dois termos (em temperaturas de 30 a 50 °C) e de Midilli (60 °C) obtiveram os melhores e mais adequados resultados para representar o processo de secagem da polpa de tucumã.

Neste contexto, o presente estudo objetivou realizar a cinética de secagem da pasta de beterraba, avaliando a influência das temperaturas de 60, 70 e 80°C aplicadas e representadas por meio da modelagem matemática a partir dos dados experimentais.

MATERIAL E MÉTODOS

A matéria-prima utilizada foi beterraba (Beta vulgaris, L.)adquirida em feira livre da cidade de Pau dos ferros e processada no laboratório de processamento de Alimentos do Instituto Federal do Rio Grande do Norte – Campus Pau dos Ferros. Em seguida selecionadas manualmente, de forma a eliminar os que apresentarem danos físicos, lavadas em água corrente e, logo após, realizada a sanitização, imergindo-se os mesmos em recipiente contendo solução de hipoclorito de sódio com concentração de 50 ppm, durante 15 min, e por fim enxaguados em água corrente para retirar o excesso da solução. As beterrabas foram trituradas integralmente (casca e mesocarpo) em liquidificados industrial para obtenção de uma pasta, a qual foi acondicionada em sacos de polietileno de baixa densidade e armazenada em freezer a –18 °C até o momento da utilização nos experimentos. A polpa foi descongelada sob refrigeração e posteriormente foi dessecada.

A secagem da pasta de beterraba foi secada em estufa com circulação de ar, na temperatura de 60, 70 e 80 °C, com espessuras da camada de 0,5 cm e velocidade do ar de 1,0 m/s. A pasta de beterraba foi espalhada uniformemente em bandejas retangulares (24,5 x 16,5 cm) de aço inoxidável formando uma camada fina. Durante a secagem as bandejas foram pesadas em intervalos de tempo regulares até massa constante. Após a secagem as amostras foram removidas das bandejas com auxílio de uma espátula de aço inoxidável e trituradas em processador (liquidificador doméstico) para obtenção das farinhas.

A partir dos dados experimentais de secagem foram calculados os valores da razão de teor de água de acordo com a Equação 1.

Em que:

RX: razão de teor de água do produto, adimensional;

X: teor de água do produto (b.s.);

X_i: teor de água inicial do produto (b.s.);

X_e: teor de água de equilíbrio do produto (b.s.).

        Na Tabela 1 estão apresentados os modelos matemáticos amplamente empregados para descrever a cinética de secagem de vegetais. O ajuste dos modelos foi realizado pela análise de regressão não linear, pelo método Quase-Newton.

Os critérios preliminares de seleção do modelo com melhor ajuste foram: coeficiente de determinação (R²), desvio quadrado médio (DQM) e o qui-quadrado médio (²), conforme equações abaixo (7 e 8).

Sendo: Y: valor de RX experimental; Ŷ: valor de RX estimado pelo modelo; n: número de observações; GLR: graus de liberdade do modelo (observações menos o número de parâmetros do modelo).

Para a determinação da difusividade efetiva, os dados da secagem foram ajustados ao modelo difusivo de Fick considerando-se a forma geométrica de placa plana, com aproximação de cinco termos, conforme Equação 9.

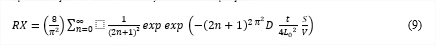
Sendo: RX: razão de teor de água, adimensional; D: coeficiente de difusão efetivo, m² s^-1; S: área da placa equivalente, m²; V: volume da placa equivalente, m³; L₀: meia espessura da massa, m; n: número de termos da equação; t: tempo, s.

Para ajustados aos dados experimentais da cinética de secagem da pasta de beterraba, utilizando-se a análise de regressão não linear, pelo método Quase-Newton, empregando-se o programa computacional Statistica 7.0®. Os critérios usados para determinação do melhor ajuste dos modelos aos dados experimentais foram: coeficiente de determinação (R2), qui-quadrado médio (²) e desvio quadrático médio (DQM).

RESULTADOS E DISCUSSÃO

Na Tabela 2 tem-se o tempo de secagem da pasta de beterraba nas diferentes temperaturas de secagem (60, 70 e 80 ºC) com velocidade do ar de 1,0 m/s. Observa-se que, com o aumento da temperatura o tempo de secagem foi reduzido.

O comportamento de redução do tempo de secagem com o aumento da temperatura ocorreu em razão da maior transferência de calor e massa que tem como consequência perda de água do produto (polpa) mais rápida. Segundo Goneli et al. (8), que relata sobre a influência da temperatura na redução do tempo de secagem, é consequência do aumento do nível de vibração das moléculas de água, contribuindo assim, para uma difusão mais rápida da água. As temperaturas na faixa de 40 a 80 ºC são as mais indicadas para secagem de materiais biológicos para que não comprometa significativamente as características nutricionais dos alimentos. O tempo de secagem pode variar de acordo com material, velocidade do ar e espessura da camada. Nascimento et al.(9) efetuou a cinética de secagem das amêndoas de girassol, avaliando a influência das diferentes temperaturas aplicadas no processo (60, 70 e 80 °C), sendo que para a temperatura de 80 °C o tempo de processo foi bem inferior, aproximadamente de 450 min.  Soares (10) efetuou a secagem da folha da batata-doce nas temperaturas de 40, 50, 60 e 70°C e nas temperaturas de 50, 60 e 70°C a secagem ocorreu de forma mais rápida, levando em torno de 540, 300 e 240 minutos, respectivamente. Nos estudos apontados nota-se que faixa de tempo de secagem é aproximada aos encontrados na secagem da pasta de beterraba. 

Nas Tabelas 3 tem-se os parâmetros dos ajustes dos modelos matemáticos aos dados experimentais da cinética de secagem da pasta de beterraba em diferentes temperaturas ( 60, 70 e 80 °C) e espessura 0,5cm com os respectivos coeficientes de determinação (R²), qui-quadrado médio (²) e desvio quadrático médio (DQM).

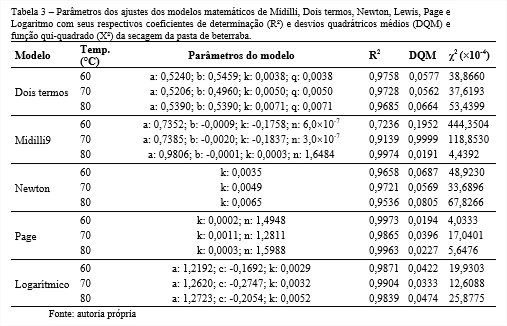
Nota-se que o modelo de Page foi o que melhor se ajustou aos dados experimentais da secagem da pasta de beterraba, nas temperaturas de 60º e 70 ºC, apresentando os maiores coeficientes de determinação (R²) variando entre 0,99816 e 0,99864 e os menores valores de X² de 4,0333 (60º), 17,0401 (70º) e 5,6476 (80º), e desvios quadráticos médios (DQM) variando entre e 0,0194 a 0,0396 indicando que este modelo representa satisfatoriamente o fenômeno de secagem da pasta de beterraba.

Os modelos matemáticos de Dois termos, Newton, Lewis e Logaritmo também apresentam bons ajustes aos dados experimentais da secagem, considerando os parâmetros de coeficientes de determinação (R²) superiores a 0,97, com exceção apenas do modelo de Midilli que obteve valores de R² que oscilaram de 0,85 a 0,99;  todos os modelos apresentam os valores de desvios quadráticos médios (DQM) abaixo de 0,19.  

Com relação ao parâmetro k (constante de secagem) da maioria dos modelos apresentou tendência de aumento com o aumento da temperatura. O valor de k depende do tipo de produto, da temperatura e da umidade relativa do ar (11).

 O coeficiente de secagem K para o modelo de Page aumentou com o aumento da temperatura, indicando estar relacionado com a difusividade efetiva no processo de secagem no período decrescente e à difusão líquida que controla o processo.

No modelo de Midilli e Page tem-se o parâmetro n, cujos valores encontrados diminuíram na temperatura intermediária (70ºC), e logo após, na temperatura de 80ºC ouve um aumento. Perez et al., (12) afirmaram que o parâmetro n está relacionado à resistência interna do material à secagem. Na Figura 1 estão representadas as curvas ajustadas como o modelo de Page aos dados experimentais da cinética de secagem da pasta de beterraba nas temperaturas de 60 ,70 e 80 °C. O modelo de Page foi considerado como o modelo que melhor se ajustou aos dados experimentais na predição das curvas de secagem da pasta de beterraba, pois apresentou o melhor ajuste aos dados experimentais.  Verifica-se que as perdas de água são maiores no início do processo de secagem; depois, as perdas são reduzidas com consequente diminuição da água presente na pasta de beterraba.

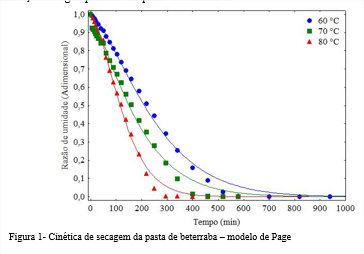
Esses resultados se encontram em estudos de diversos autores que avaliaram a temperatura do ar de secagem como o parâmetro que exerce maior influência na cinética de secagem de alimentos, dentre eles: Almeida et al. (13) ao realizarem a cinética de secagem de fatias de beterraba em diferentes espessuras (4, 6 e 8 mm) na temperatura de 60°C, também determinaram que o modelo matemático de Page foi o que melhor se ajustou aos dados experimentais.

Araújo et al. (14) efetuaram a secagem das sementes da pitaya vermelha (Hylocereus polyrhizus) em um secador nas temperaturas de 50, 60 e 70°C e velocidades do ar de desidratação de 0,55 e 0,75 m s^-1. Dentre os modelos matemáticos utilizados para a determinação da cinética de secagem, o de page foi o que melhor representou os dados experimentais.

Na Tabela 4, está apresentado o valor médio da difusividade efetiva (D_ef), obtidos na secagem da pasta de beterraba na espessura 0,5 cm e nas temperaturas de 60, 70 e 80 °C, calculado conforme a lei de Fick para uma placa plana, logo a difusividade aumentou com a elevação da temperatura. A difusividade é a facilidade com que a água é removida do material e pode variar conforme as condições de secagem (temperatura e velocidade do ar) e não é intrínseca ao material (15).

Furtado et al. (16) na secagem em camada de espuma da polpa de abacaxi Pérola nas temperaturas de 60, 70 e 80 °C encontraram difusividades efetivas de 0,810569 x 10^-9,1,45903 x 10^-9 e 1,94537 x10^-9 m²/s, respectivamente. Portanto, os resultados se encontram equivalente ao encontrado para pasta de beterraba.

Lisboa et al. (17) realizaram a difusividade efetiva da batata yacon, verificou-se que a difusividade efetiva aumentou com o aumento da temperatura, variando de 1,18 x 10^-9 a 2,15 x 10^-9 m² s^-1 em todas as temperaturas estudadas.

CONCLUSÕES

Com o aumento da temperatura do ar ocorre redução no tempo de secagem da pasta de beterraba.

 O modelo de Page é o que melhor se ajusta aos dados nas diferentes condições de secagem da pasta de beterraba. Na difusividade efetiva houve um aumento com aumento da temperatura.

REFERÊNCIAS

1.  Santos MLPL, Mota BB, Schirmann G, Braganca GCM, Verbes M P,  Lima N F, et al. Características de consumo e aproveitamento integral da beterraba (Beta Vulgaris). Res. Braz. Jour. Dev, 2021, 7: 79770-79780.

2. Oliveira LP, Cesconetto G, Schveitze B, Foppa, T. Avaliação e composição nutricional da farinha de beterraba e sua utilização no preparo de sobremesas. Rev.Interd. de Est. Saúde, 2013,1: 13-19.

3. Resende O, Corrêa PC, Goneli ALD, Botelho FM, Rodrigues S. Modelagem matemática do processo de secagem de duas variedades de feijão (Phaseolus vulgaris L.). Rev. Bras. de Prod. Agroind., 2008, 10: 17-26.

5. Resende O, Ullmann R, Siqueira VC, Chaves TH, Ferreira LU. Modelagem matemática e difusividade efetiva das sementes de pinhão-manso (Jatropha curcas L.) durante a secagem. Rev. de Eng. Agrícola, 2011, 31: 1123-1135.

6. Silva A S A, Melo KS, Alves NM, Fernandes T K S, Farias P. A. Cinética de secagem em camada fina da banana maçã em secador de leito fixo. Rev. Bras. de Prod. Agroind., 2009, 11: 129-136.

7. Pereira C B, Souza J B, Santos D. C, Leite D D F, Ferreira J P L, Oliveira E N A. Modelagem matemática e propriedades termodinâmicas da secagem convectiva da polpa de tucumã (Astrocaryum aculeatum). Rev.  Holos, 2022, 1: 1-18.

8. Goneli A L D, Corrêa P C, Afonso Júnior P C, Oliveira G H H. Cinética de secagem dos grãos de café descascados em camada delgada. Rev. Bras. de Armazenamento, 2009, 11: 64-73.

9.  Nascimento A P S, Barros, S. L, Santos N C, Araújo A J B, Cavalcanti A S R R M, Duarte M E M. Secagem convectiva e influência da temperatura nas propriedades físico-químicas das amêndoas de girassol comercial. Rev. Bras. de Prod. Agroind, 2018, 20:  227-238.

10. Soares AH. Estudo experimental e modelagem matemática do processo de secagem da folha de batata-doce (Ipomoea batatas). Trabalho de Conclusão de Curso. Paraná:  Universidade Tecnológica Federal do Paraná, 2021.

11. Carlesso VO, Berbert  PA,  Silva RF,  Detmann E. Avaliação de modelos de secagem em camada fina de sementes de maracujá amarelo. Rev. Bras. de Sementes,2007, 29: 28-37.

12.  Perez LG, Oliveira F M N, Andrade J S, Moreira Filho M. Cinética de secagem da polpa cupuaçu (Theobroma grandiflorum) pré-desidratada por imersão-impregnação. Rev. Ciênc. Agron, 2013, 44:102-106.

13. Almeida R L J, Santos N C, Silva V M A, Ribeiro VHA, Barros ER, Cavalcante, JA, et al. Influência da espessura na cinética de secagem de fatias de beterraba. Res. Soc. Dev., 2020, 9:  e18942940.

14. Araújo KTA, Figueirêdo R M F, Queiroz A J M, Silva RC, Paiva Y F, Amadeu L TS, et al. Cinética de secagem de pitaya vermelha (Hylocereus polyrhizus). Res., Soc. Dev.,2021, 10: 357101220630.

15. Oliveira RA, Oliveira W P, Park KJ. Determinação da difusividade efetiva de raiz de chicória. Rev. Eng.Agrícola, 2006, 26:181-189.

16. Furtado GF,  Silva FS,  Porto AG,  Santos, P. Secagem de abacaxi (Ananas comosus (L.) Merril), variedade pérola utilizando a técnica de camada de espuma. Rev. Bras. de Prod. Agroind, v.16, n.4, p.387-394, 2014.

17. Lisboa, C. G. de, Gomes, J. P., Figueirêdo, R. M. de, Queiroz, A. J. D. M., Diógenes, A. D. M., & Melo, J. . Effective diffusivity in yacon potato cylinders during drying. Rev. Bras. de Eng. Agrícola e Ambient, 22(8), 564-569, 2018.